Elixirでダイクストラ法を実装して最短経路を求めるまで

グラフと最短経路

こんなグラフのネットワークがあったとする

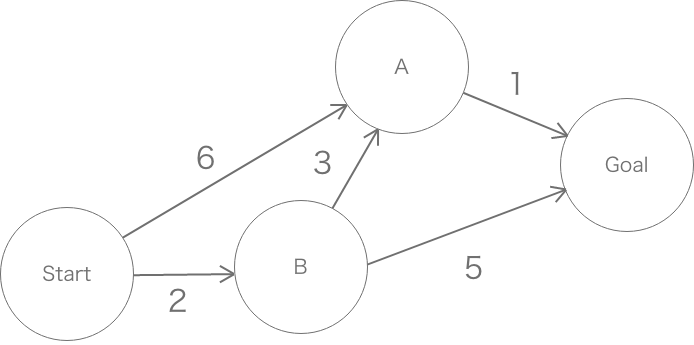
Start, A, B, Goalをそれぞれノードといい
6,2,3...のような数字をエッジの重み(ここでは距離)という

StartからGoalへの最短経路は見て分かるように

Start -> B -> A -> Goal

になるかと思う

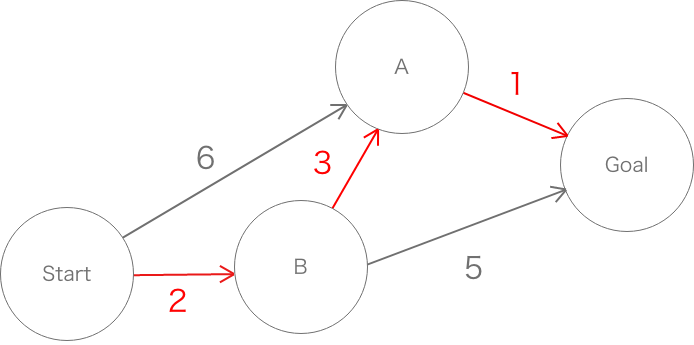
これがこのグラフでのStartからGoalへの最短経路となる

ではこの最短経路をアルゴリズム使って求められへんの？っていう賢い人が現れる
それで開発されたのがダイクストラ法というアルゴリズム

しかし説明をすると長くなる & 図が大量に必要なので省略する
(すでに書籍や先駆者の有志の方が最高に分かりやすい説明をしてくださっているため)

「ダイクストラ法　解説」　などで検索してみてください

データ構造について

まずはデータの構造を定める
ここ数日、アルゴリズムの実装をして感じていることは
アルゴリズムのロジックを組む際の難易度はデータ構造に大きく依存するということ

シンプルなデータ構造で表現できた場合にはコードはあまり複雑にならない
データ構造に無駄があったり、欠陥があるとその分、コード部分で苦労をする

「このデータ構造が最もふさわしい」というベストアンサーは決めにくいが
シンプルであればシンプルであるほど良いというのが自分の中での答えかなと思ってます

ダイクストラ法に必要な3つのデータ

• グラフ情報(graph)
• コスト情報(costs)
• 親ノード情報(parents)

をそれぞれ以下のように定めた(書籍を参考に実装した)

グラフ情報

#それぞれのノードがどのノードに接続しているか(距離も付与)
#start: %{a: 6, b: 2},
#start --6--> a
#start --2--> b ということを表現している
graph = %{
  start: %{a: 6, b: 2},
  a: %{fin: 2},
  b: %{a: 3, fin: 5},
  fin: %{}
}

コスト情報

#startから接続しているノードまでの距離
#startと接続していないノードにはinfinityをセット
costs = %{
  a: graph.start.a,
  b: graph.start.b,
  fin: :infinity
}

親ノード情報

#startから接続しているノードのノード名
#そのほかはnilとしておく
parents = %{
  a: :start,
  b: :start,
  fin: nil
}

1つにまとめられそうな気もするが、あまり複雑化させるよりはいくつかに分別して方が経験上良い
データの準備は以上で次にコードを実装する

Elixirでのダイクストラ法の実装

まずは全体のコードをお見せします

defmodule Algo do
  def dijkstra(graph, costs, parents, processed) do
    node = _search_minimize_cost_in_graph(costs, processed)
    case node do
      :empty -> {costs, parents}
      _ ->
        neighbors = graph[node]
        {n_costs, n_parents} = _node_update(node, Map.keys(neighbors), costs[node], costs, neighbors, parents)
        dijkstra(graph, n_costs, n_parents, processed ++ [node])
    end
  end

  defp _node_update(_, [], _, costs, _, parents), do: {costs, parents}
  defp _node_update(node, [head | tail], cost, costs, neighbors, parents) do
    new_cost = cost + neighbors[head]
    if costs[head] > new_cost do
      n_costs = Map.put(costs, head, new_cost)
      n_parents = Map.put(parents, head, node)
      _node_update(node, tail, cost, n_costs, neighbors, n_parents)
    else
      _node_update(node, tail, cost, costs, neighbors, parents)
    end
  end
  
  def creater(res, start_atom, end_atom) do
    _creater(res, start_atom, end_atom, [end_atom])
  end
  def _creater(res, start_atom, next_atom, accum) do
    end_val = res[next_atom]
    if end_val == start_atom do
      [start_atom] ++ accum
    else
      _creater(res, start_atom, end_val, [end_val] ++ accum)
    end
  end

  defp _search_minimize_cost_in_graph(costs, processed) do
    rest_node = Map.keys(costs) |> Enum.filter(fn x -> x not in processed end)
    case rest_node == [] do
      true -> :empty
      false -> Enum.reduce(rest_node, :infinity, fn x, accum ->
        if accum > costs[x] do
          x
        else
          accum
        end
      end)
    end
  end
end

この先の説明部分については完全に自己満足なので
結果を先にお見せします

graph = %{
  start: %{a: 6, b: 2},
  a: %{fin: 1},
  b: %{a: 3, fin: 5},
  fin: %{}
}

costs = %{
  a: graph.start.a,
  b: graph.start.b,
  fin: :infinity,
}

parents = %{
  a: :start,
  b: :start,
  fin: nil
}

res = Algo.dijkstra(graph, costs, parents, [])
#res: {%{a: 5, b: 2, fin: 6}, %{a: :b, b: :start, fin: :a}}

{_a, b} = res
root = Algo.creater(b, :start, :fin)
#root: [:start, :b, :a, :fin]

別のグラフで試してみる

graph = %{
  start: %{a: 6, b: 2, c: 1},
  a: %{fin: 1},
  b: %{a: 3, fin: 5},
  c: %{a: 6, fin: 2},
  fin: %{}
}

costs = %{
  a: graph.start.a,
  b: graph.start.b,
  c: graph.start.c,
  fin: :infinity,
}

parents = %{
  a: :start,
  b: :start,
  c: :start,
  fin: nil
}

res = Algo.dijkstra(graph, costs, parents, [])
{_a, b} = res
root = Algo.creater(b, :start, :fin)

#root: [:start, :c, :fin]

良い感じですね 実装についてはここまでです
どんな動きをしているかが気になる方は以下をどうぞ

作成したモジュールについて

最短経路を求めるこのモジュールは4つの関数から成り立っている

• dijkstra(メイン関数)
• _node_update(条件に従いノード情報を更新する関数)
• creater(dijkstraの結果から最短経路を作成する関数)
• _search_minimize_cost_in_graph(最も手数が少ないノードを探索する関数)

順にコードを見ていく

dijkstra

def dijkstra(graph, costs, parents, processed) do
    #隣接しているノードの中で最も距離が近い(コストが低い)ノードを探索
    node = _search_minimize_cost_in_graph(costs, processed)
    case node do
      #もう探索できるノードがない場合
      :empty -> {costs, parents}
      _ ->
        #探索した最もコストの低いノードに隣接しているノードを取得(マッチ)
        neighbors = graph[node]
        #ノード情報をアップデート
        {n_costs, n_parents} = _node_update(node, Map.keys(neighbors), costs[node], costs, neighbors, parents)
        #今調べたノードを探索済み(accumに追加)して再帰
        dijkstra(graph, n_costs, n_parents, processed ++ [node])
    end
end

_node_update

#探索できるノードが無くなったら終了
defp _node_update(_, [], _, costs, _, parents), do: {costs, parents}
defp _node_update(node, [head | tail], cost, costs, neighbors, parents) do
  #次のノードまでの合計距離
  new_cost = cost + neighbors[head]
  #現時点で発見されているコストよりも別ルートの方が最短かどうか
  if costs[head] > new_cost do
    #コスト情報と親情報を上書き
    n_costs = Map.put(costs, head, new_cost)
    n_parents = Map.put(parents, head, node)
    _node_update(node, tail, cost, n_costs, neighbors, n_parents)
  else
    _node_update(node, tail, cost, costs, neighbors, parents)
  end
end

_node_updateが呼ばれる以前にこんなことが起きている

• Startから最もコストが低いノードはBノード
• Bノードに隣接しているノードを全て取得(Aとfin)

この情報を元に_node_updateが呼ばれる
例えばBノードからAノードへの探索をする場合には元々のコストは以下のようになっている

ノード名	距離(コスト)
A	6
B	2
fin	infinity

しかし、_node_updateが呼ばれ現状のAルートへの道のりよりも
Bを経由してAに行った方が近いことが分かる

head = :a #Aノード
new_cost = cost + neighbors[head]
#new_cost = 2 + 3 -> 5
#このコストは現状の6よりも小さい

従ってコストを更新する

ノード名	距離(コスト)
A	5
B	2
fin	infinity

さらに親ノードの情報も更新する
更新前

ノード名	距離(コスト)
A	start
B	start
fin	infinity

更新後

ノード名	距離(コスト)
A	B
B	start
fin	nil

creater
この関数についてはオマケなのであまり深く語る部分はない
dijkstraの戻り値の第2要素を使ってresからrootを生成しているだけ

res = %{a: :b, b: :start, fin: :a}
root = Algo.creater(res)

iex> root
[:start, :b, :a, :fin] #道順になっている

_search_minimize_cost_in_graph

defp _search_minimize_cost_in_graph(costs, processed) do
  #探索済みのノードを破棄
  rest_node = Map.keys(costs) |> Enum.filter(fn x -> x not in processed end)
  case rest_node == [] do
    true -> :empty
    #[:a, :b, :fin]から最小コストを持つノードを探索
    false -> Enum.reduce(rest_node, :infinity, fn x, accum ->
      if accum > costs[x] do
        x
      else
        accum
      end
    end)
  end
end

長くなってしまいましたが、おそらくコード自体はもっと短くできるかと思います
とりあえずは実装してみるを原動力に書いているのでその点はご了承ください。リファクタリングはElixir力が高まってからチャレンジしてみようと思います